Les sphères

Les sphères
La sphère, écrit Platon dans le Timée, est « de toutes les figures, la plus parfaite et la plus semblable à elle-même ». La sphère est une forme géométrique simple dont le monde qui nous entoure offre de nombreux exemples. Elle paraît banale et, à première vue, on pourrait se demander ce qu’il peut bien avoir a dire à son propos.
Mais sous le concept familier de sphère se cache un objet aux « multiples » facettes mathématiques et physiques.
Du point de vue de la géométrie euclidienne, la sphère est l’ensemble des points de l’espace à trois dimensions qui se trouvent a à la même distance d’un point fixé. Pour la définir, ne sont donc requis que la donnée d’un point, son centre, et de son rayon.
Les sphères sont impliquées dans de nombreuses questions d’optimisations, comme le problème de l’empilement le plus compact de sphères, c'est-à-dire qui laisse le moins d’interstices entre elles (c’est la conjecture de Kepler, et elle vient juste d’être démontrée) ; et aussi celui d’inégalité isopérimétrique, c'est-à-dire le fait que la sphère est le solide qui a le volume maximal pour une surface donnée.
Cette affirmation est appelée théorème de Didon, à cause d’une légende grecque.

Le théorème de Didon
Le poète Virgile raconte dans l’Eneide Que la reine Didon (pour fonder Carthage au 9ème siècle avant J-C), acheta de la terre au roi de Numidie. Le roi n’avait pas envie de cette intrusion, mais il consentit à lui octroyer la terre que pouvait contenir une seule peau de bœuf.
Didon, femme avisée et mathématicienne avant l’heure, tira le meilleur parti possible de la situation : elle découpa la peau en fines lamelles, pour en faire une corde de 2000 mètres environ. Elle devait donc trouver, parmi toutes les courbes fermées, celle qui délimite la plus grande surface possible. Ce genre de problème s'appelle problème isopérimétrique.
Didon comprit que la solution était un cercle. Nous appellerons ce résultat le « théorème de Didon ».
Il a fallu de nombreuses années aux mathématiciens pour démontrer ce théorème. On peut quand même établir quelques éléments de cette démonstration.
Nous admettons qu’il existe une solution, c'est-à-dire une courbe de longueur donnée qui rende la surface incluse maximale. Montrons d’abord que cette courbe (de longueur fixe) doit délimiter une surface convexe.

Sinon, supposons qu’on ait quelque part cette situation. On peut trouver deux points A et B sur la courbe tels que tout le segment AB soit à l’extérieur de la courbe.

Par symétrie, on peut alors remplacer le segment de courbe (C) par une courbe (C’)qui a la même longueur que (C) mais qui enferme une plus grande surface. (sphere002) Donc nécessairement le segment de courbe C qui donne la surface maximale doit être convexe.

En raisonnant par l’absurde, on a ainsi démontré que la surface maximale enfermée par une courbe de longueur donnée est un cercle.
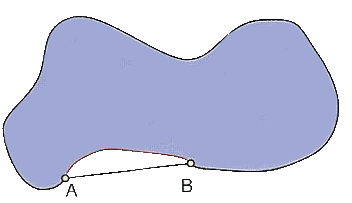
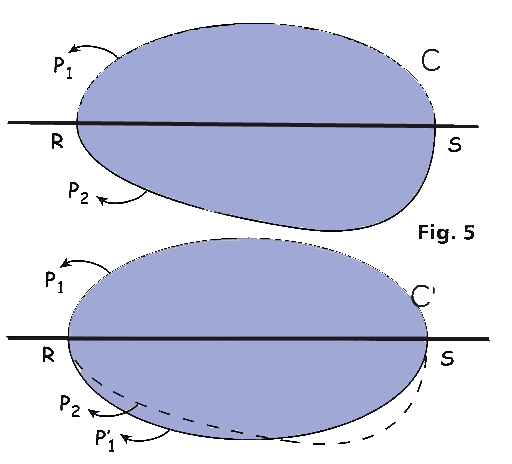
Si la démonstration paraît assez simple dans le plan, elle est bien plus ardue dans l’espace, car en fait, dans le plan, la longueur d’une courbe est simplement la limite des périmètres des polygones inscrits dans la courbe quand on augmente le nombre de côtés. En revanche, dans l’espace, la notion d’aire d’une surface générale n’est pas facile à modéliser, et, pour les domaines d’un certain type, l’inégalité isopérimétrique devient fausse.
Si on considère des domaines convexes, la démonstration de l’inégalité isopérimétrique devient plus facile, mais l’unicité reste difficile. Avant tout, in faut définir l’aire de surface. Pour les formes convexes, il suffit de faire des approximations par des polyèdres, l’aire est alors la limite des surfaces des polyèdres inscrits quand on augmente le nombre de faces.
La démarche de Steiner pour démontrer l’inégalité isopérimétrique consiste à symétriser le solide par rapport à un nombre croissant de plans, comme nous l’avons fait plus tôt dans le plan. On montre ainsi que le volume est préservé, que l’aire ne peut que diminuer, et que finalement il y a forcément un objet limite, qui est nécessairement la sphère. Le problème de cette manière de faire, c’est qu’on ne prouve pas le fait que la sphère soit le seul objet pour lequel l’égalité est établie.
Il s’avère que la seule manière de démontrer rigoureusement l’inégalité isopérimétrique, c’est d’utiliser la théorie géométrique de la mesure, qui permet notamment de prouver, car on ne l’a pas fait jusque là, qu’il existe des objets qui ont le volume maximal pour une surface donnée.

A notre niveau, on peut déjà comparer par exemple le rapport entre la surface et le périmètre d'un cube d'une sphère :

On constate donc bien que pour une surface donnée S, le volume V est plus grand dans le cas de la sphère.